ACM – Active Connections Matrix (International Patent)
The relevant topology of a phenomenon is its intrinsic geometry expressing the form which can be taken from the frequency spectra where the phenomenon is analyzed and from the respective variations of energy. These variations of energy become relevant information because they are expression of the relevant topology of the phenomenon that is to say of its form or intrinsic geometry. In this case the phenomenon is called visual phenomenon.
Every relevant topology phenomenon has identity and unity of the phenomenon itself granted by its space-time cohesion. This means that each minimal element of the phenomenon is directly or indirectly contiguous and connected by specific forces to the others. Therefore the quantitative value of each minimal element of the analyzed phenomenon results from the action of these forces. It can be demonstrated that in a relevant topology phenomenon the forces connecting each minimal elements to each other in its local neighborhood are enough to explain the space-time cohesion of the whole phenomenon.
This allows saying that each visual phenomenon can be expressed as a matrix of values, locally connected each other, by other values (weights), representing the local cohesion forces of the minimal units of that phenomenon.
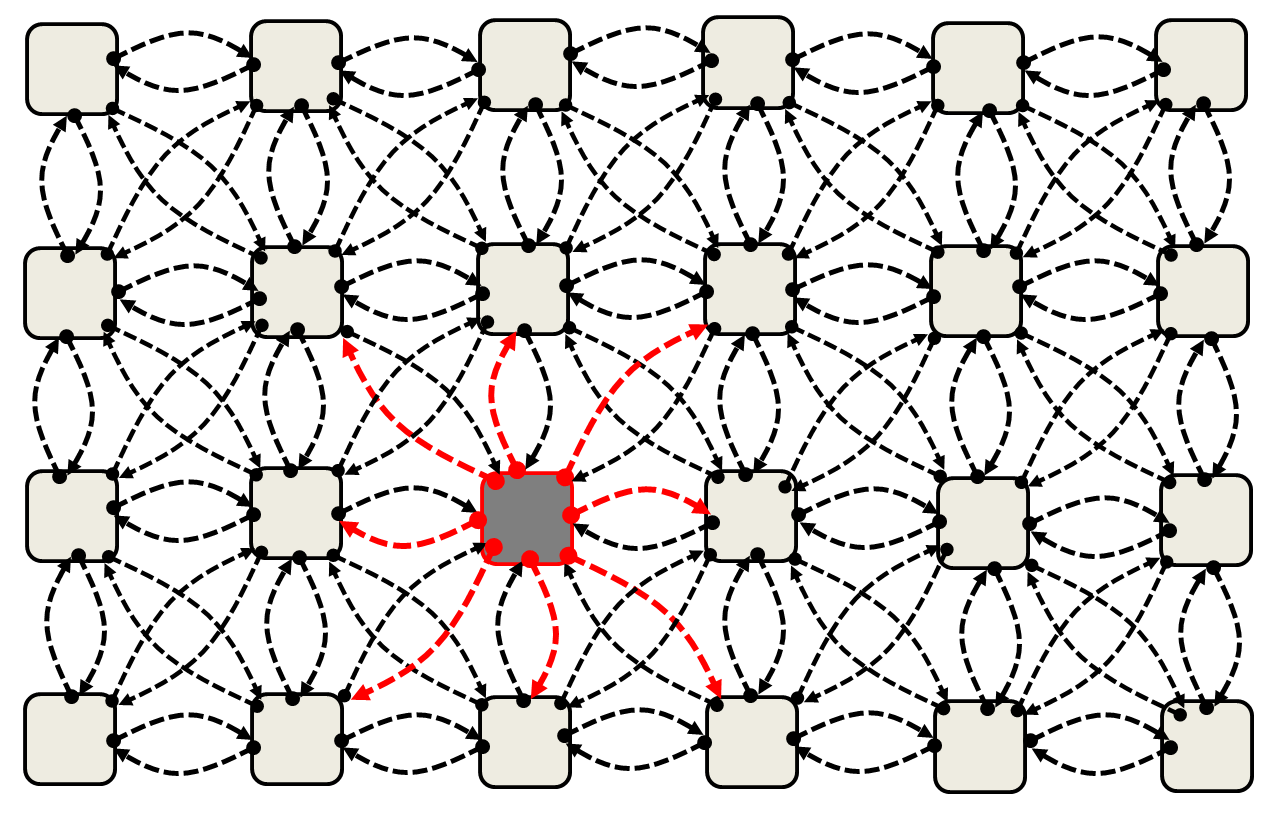
The phenomenon we refer in general in our research to, concerns the image caught by our sensibility when a light-shrouded subject appears to us precisely as a phenomenon. The image of the subject caught and made available as phenomenon, can be represented for its analytic treatment by a matrix of points corresponding to the pixels the assumed initial image. Trying to extract from this image, that is to say from this phenomenon, other information about the subject producing it, not visible in the image considered at the beginning, allows us considering the matrix of pixels of the initial image as a dynamic system developing in its phase space until it creates a final configuration matrix of the pixels. It is important not to mistake this phase space with the two-dimensional or three-dimensional space of the initial image. In fact, it is the other dimension given by the intensity of the connection forces of the pixels to each other which is added to the dimension of the latter space, when the point matrix is considered and when it is considered active meaning that the initial matrix will tends to a final matrix precisely because of a dynamic evolution of these connections.
The functioning of ACM systems is based on local, deterministic e iterative operations. They are Local, because in each elaboration cycle the operations involve a central pixel and its relations with the very contiguous pixels (neighborhood of the central pixel). They are Deterministic, because the static state, towards which the dynamic system represented by the matrix of pixels with the new image tends, is based on deterministic equations: therefore the elaboration can be repeated getting always the same result. They are Iterative, because the operations are repeated iteratively until the evolution in the space of phases, of the dynamic system, reaches its attractor.
Patents:
Buscema P.M.(2003) European patent “An algorithm for recognizing relationships between data of a database and a method for image pattern recognition based on the said algorithm” (Active Connection Matrix –ACM). Owner: Bracco, Semeion. Application no. 03425559.6, deposited August 22, 2003.
Buscema P.M. (2004) International patent “An algorithm for recognizing relationships between data of a database and a method for image pattern recognition based on the said algorithm” (Active Connection Matrix – ACM). Owner: Bracco, Semeion. Application n. PCT/EP2004/05182, deposited: August 18, 2004.
Buscema P.M. (2007) European patent “Active Connection Matrix J-Net. An algorithm for the processing of images able to highlight the information hidden in the pixels”. Owner: Bracco, Semeion. Application n. 07425419.4, deposited: July 6, 2007.
References:
P.M. Buscema et al. (2006) Sistemi ACM e imaging diagnostico. Le immagini mediche come matrici attive di connessioni [ACM systems and diagnostic imaging. Medical images as active connections matrices, in Italian] Springer-Verlag, Italy.
P.M. Buscema, L. Catzola, E. Grossi (2008) Images as active connection matrixes: the J-Net system. IC-MED Int J Intell Comput Med Sci 2(1):27–53.
P.M. Buscema, R. Passariello, E. Grossi, G. Massini, F. Fraioli, G. Serra (2013) , J-Net: An Adaptive System for Computer-Aided Diagnosis in Lung Nodule Characterization, chapter 2, pp 25-61, in W.J. Tastle (ed.), Data Mining Applications Using Artificial Adaptive Systems, Springer Science+Business Media New York 2013.
